Скачать книги жанра Математика
Представленные в пособии игры, задания и упражнения с использованием геометрических фигур мозаики способствуют формированию у детей логического и математического мышления, развитию мелкой моторики рук; стимулируют развитие важнейших психических процессов, необходимых для успешного обучения в школе.
Книга адресована воспитателям дошкольных образовательных учреждений, учителям начальной школы и родителям.
Эта книга способна в корне изменить ваше отношение к математике. Она состоит из коротких глав, в каждой из которых вы откроете для себя что-то новое. Вы узнаете насколько полезны числа для изучения окружающего мира, поймете, в чем прелесть геометрии, познакомитесь с изяществом интегральных исчислений, убедитесь в важности статистики и соприкоснетесь с бесконечностью. Автор объясняет фундаментальные математические идеи просто и элегантно, приводя блистательные примеры, понятные каждому.
На русском языке публикуется впервые.
Работа посвящена проблемам этико-правовых систем, созданных обществом для обеспечения человеческой деятельности. Рассматриваются методы и средства синтеза и анализа этико-правовых систем, создающих этико-правовой потенциал общества.
Разрабатываются теоретические основы формирования систем минимизации рисков и максимизации эффективности функционирования этико-правовой системы при создании этико-правового потенциала.
В основу математического моделирования этико-правового риска положены качественные модели формирования этико-правового потенциала, с помощью которых формируется структурно-функциональный синтез, а затем анализ системы.
В монографии представлены материалы, полученные автором в области качественных и количественных моделей риска и безопасности функционирования коммерческих банков. Значительное внимание уделено качественным моделям систем управления как основе структурно-функционального синтеза рассматриваемых систем, которые в свою очередь создают условия для структурно-функционального анализа, включающего математическое моделирование. При этом решающее значение имеют не только системы управления, но и системы контроля. Материалы, представленные в работе, дополняют и развивают модели, разработанные международными организациями, которые представлены в Базель-2.
Американский математик, исследователь в области теории чисел Эрик Т. Белл посвятил свою книгу истории происхождения математической мысли и разработки численной теории с момента ее зарождения в древности до современной эпохи. Обоснованно и убедительно автор демонстрирует влияние, которое оказала «магия чисел» на развитие религии, философии, науки и математики. Э.Т. Белл рассматривает процесс превращения числа из инструмента счета в объект культуры, сформировавшийся в VI веке до н. э. в школе древнегреческого философа, мистика, физика-экспериментатора и математика Пифагора – главного героя его исследования. Основополагающим моментом учения великого ученого древности стала доктрина о том, что «все сущее есть число». Доктор Белл изучил развитие этой доктрины: ее упадок в XVII веке и блистательное возрождение в современной физике. Автор также представил и проанализировал труды таких гигантов математики, как Галилей, Джордано Бруно, Ньютон.
Вводный курс для начинающих изучать язык Java. Быстрый и ощутимый результат – лучший стимул в обучении. Занимаясь 1—2 часа по вечерам, уже через неделю вы будете писать полноценные оконные приложения с графическим интерфейсом. Книга содержит примеры с пошаговыми пояснениями. Приведен список литературы для желающих продолжить обучение. Работа с учебными проектами полностью ведется в современной визуальной среде разработки NetBeans IDE. Книгу дополняет файловый архив с исходными кодами примеров.
496 примеров на деление натуральных чисел с ответами.Задания отсортированы по возрастанию трудности вычислений.Книга будет полезна при подготовке к ВОУД, ВПР, ГИА, ЕНТ, ЕГЭ, SHL-тестам, Formatta, "Числовые тесты", "IQ тесты" для успешной сдачи экзаменов и трудоустройства в в Big4, Procter & Gamble, Schlumberger, Mars, Unilever, BAT, Pepsi, Nestle, Henkel, JTI, Philip Morris и другие компании.
Математика больше не будет казаться скучной наукой! Математические фокусы повышают интерес к математике и развивают математические способности у ребенка.А еще с этой книгой он почувствует себя настоящим волшебником!
В научном комиксе «Пирамида чисел Фибоначчи – Кучина» автор в популярной форме рассказывает читателю о том, как выполнить это удивительное арифметическое построение, и дает основные примеры калибровки объектов в окружающем нас мире по числам из этой пирамиды. Книга предназначена для широкого круга любознательных читателей всех возрастов.
В данной книге описан простой способ, как заглянуть в будущее математическим способом. Книга полезна начинающим статистам, математикам, читателям, работающим с данными, отделам контроля продаж.
Приведено доказательство векторной природы гравитационного потенциала, согласно которой гравитационный потенциал в любой точке бесконечной Вселенной равен нулю. Напротив, согласно скалярным представлениям о гравитационном потенциале, в стационарной Вселенной гравитационный потенциал равен бесконечности, причём в любой точке пространства. Однако этот потенциал входит в уравнение всемирного тяготения, имеющего явно векторный характер. Закон неявно содержит в себе не только ускорение свободного падения, векторную величину, но и формирующий его гравитационный потенциал, который автоматически получает статус вектора.
Считается, что одним из главных аргументов, из которого следует вывод об ускоренном расширении Вселенной, является пониженная яркость дальних сверхновых. Математическое исследование этого явления неожиданно привело к прямо противоположному выводу. Если дальние сверхновые видны более тусклыми, то Вселенная расширяется с замедлением. It is believed that one of the main arguments from which the conclusion about the accelerated expansion of the Universe follows is the reduced brightness of distant supernovae. A mathematical study of this phenomenon unexpectedly led to the exact opposite conclusion. If distant supernovae are seen dimmer, then the universe is expanding decelerate.
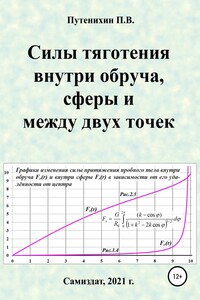
Рассмотрены силы, действующие на пробное тело внутри обруча, полой сферы и между двумя массивными точками. По мере удаления от центра системы сила притяжения растёт от нуля до некоторого максимума. Утверждение об отсутствии сил тяготения внутри полой сферы является ошибочным. The forces acting on a test body inside a hoop, a hollow sphere, and between two massive points are considered. With distance from the center of the system, the force of attraction grows from zero to a certain maximum. The statement about the absence of gravitational forces inside the hollow sphere is erroneous.
Пожалуй, одним из самых главных наблюдаемых параметров всех космологических объектов является так называемое красное смещение, на основании которого сделан вывод о расширении Вселенной. В работе рассмотрена сущность этого явления. Perhaps one of the most important observable parameters of all cosmological objects is the so-called redshift, on the basis of which the conclusion was made about the expansion of the Universe. The essence of this phenomenon is considered in the work.
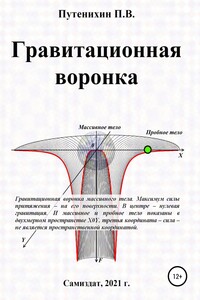
Во многих учебниках и статьях при объяснении сущности искривления пространства-времени, приводящего к возникновению гравитационной силы, силы притяжения используется метафора резинового листа. На лист помещают массивное тело и показывают, как другие мелкие тела скатываются к нему по искривлённой поверхности мембраны. Однако эта метафора вводит в заблуждение, создавая ощущение трёхмерности конструкции. В этом случае мелкие тела могут скатываться только под действием гравитации. Объяснение гравитации с привлечением гравитации – это некорректный способ. Прогиб резинового листа на самом деле не связан с третьим измерением. На самом деле изгиб мембраны следует рассматривать как функцию силы притяжения. Этот прогиб мембраны мы называем гравитационной воронкой, буквально – трёхмерным графиком силы. Все тела в этой конструкции могут двигаться только по плоскости двух координат, никакого скатывания в воронку быть не может.
Начало XXI века ознаменовано выходом в свет прекрасной книги Mathematical Models in Biology An Introduction / Elizabeth S. Allman, University of Southern Maine, John A. Rhodes, Bates College, Maine, содержащей обзор достижений века предшествующего, которая легла в основу данного издания, поэтому если уже знакомы с ней, то мне вас практически нечем удивить. В противном случае – добро пожаловать в чудесный мир тесного переплетения идей биологии, криптографии, абстрактной общей алгебры, конкретной дискретной математики и вероятностной математической статистики, на пользу бурно развивающейся ныне биоматематики. Хотите узнать в чём практический смысл вычисления собственных значений и собственных векторов матриц? Как определяется доля населения, которая должна быть успешно вакцинирована для обеспечения коллективного иммунитета? Как из структуры ДНК можно почерпнуть принципы СУВ? И много-многое другое? Тогда эта книга именно для вас.